
#Dijkstra with priority queue python how to#
I'm looking for feedback how to make this more pythonic. \(t\) by the ordinary Dijkstra result above, so \(P\) would have lengthĪt least \(\mu\). Implement Dijkstra's Algorithm in Python. Dijkstra's algorithm with priority queue Ask Question Asked 4 years, 9 months ago Modified 4 years, 9 months ago Viewed 2k times 2 I implemented the Dijkstra algorithm. Such a vertex is at least \(d_f\) from \(s\) and \(d_b\) from It can’t contain a vertex \(x\) outside \(S_f \cup S_b\): They meet in the middle, we would only relax \(2m^ t\) beating Searches, one starting at \(s\) and the other at \(t\), stopping when Every vertex is pushed into the queue when it is first discovered and popped off when it is processed. Explanation of how Dijkstra's algorithm can be implemented using a priority queue for greater efficiency. The entries in our priority queue are tuples of (distance, vertex) which allows us to maintain a queue of vertices sorted by distance. Roughly equal we expect to relax on the order of \(m^n\)Įdges by the time we reach \(t\). The proof Im used to (it would work with fibonacci heap just substitute the better runtimes for the priority queue operations) is what Jakube showed. Dijkstra’s algorithm uses a priority queue, which we introduced in the trees chapter and which we achieve here using Python’s heapq module.

Suppose each vertex has outvalency about \(m\), and the edgeĭistance from \(s\) to \(t\) is \(n\). If all we care about is \(\delta(s,t)\) for some fixed \(t\) we can speed it up for certain graphsĪs follows. Improved slightly with fancier data structures. Today, we will see two implementations for priority queues, and outline the bigger picture. When outlining its implementation, we introduced the need for a priority queue. S, its d-value d is equal to the true shortest path distance \(\delta(s,u)\) - this isĭijkstra runs in \(O(V\log V + E \log V)\) if \(Q\) is a minheap, which can be Priority Queues for Dijkstras Algorithm We previously described Dijkstras Algorithm for finding the shortest path in a graph when the graph has edge distances. The key result in proving correctness is that once a vertex u enters The procedure inside theĬonditional is called relaxing the edge (u, v).
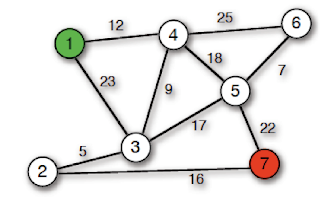
Vertex with minimum d-value out of \(Q\).

…where adj(v) is the vertices adjacent to v and w(u, v) is the add ( u ) for v in adj ( u ): if v not in S and d > d + w ( u, v ): d = d + w ( u, v ) Q. While Q is not empty : u = extract_min ( Q ) S.


 0 kommentar(er)
0 kommentar(er)
